微信公众号：路人zhang
网站救助计划

1.为阅读体验，本站无任何广告，也无任何盈利方法，站长一直在用爱发电，现濒临倒闭，希望有能力的同学能帮忙分担服务器成本


2.捐助10元及以上同学，可添加站长微信lurenzhang888，备注捐助，网站倒闭后可联系站长领取本站pdf内容


3.若网站能存活下来，后续将会持续更新内容

当前位置： 算法 > 剑指offer > 剑指offer 12.矩阵中的路径

剑指offer 12.矩阵中的路径

题目描述

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

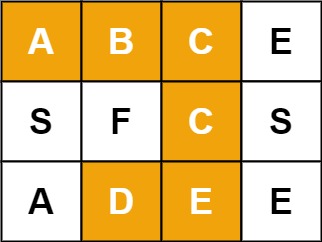
例如，在下面的 3×4 的矩阵中包含单词 “ABCCED”（单词中的字母已标出）。

示例 1：

输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出：true

示例 2：

输入：board = [["a","b"],["c","d"]], word = "abcd"
输出：false

提示：

  • 1 <= board.length <= 200
  • 1 <= board[i].length <= 200
  • board 和 word 仅由大小写英文字母组成

算法

(DFS,回溯) O(nm*3^k)

从图中每个点作为起点开始搜索长度为 word.size() 的序列，如果匹配成功则返回 true，否则从下一个点开始搜索，直到所有点作为起点都没有匹配成功，则返回 false。

搜索的逻辑：

  1. 递归函数的含义：bool dfs(int x, int y, int u, string word)，(x, y) 表示当前正在搜索的坐标，u 表示当前正在匹配 word 中的哪个字母。
  2. 递归的出口条件：如果当前坐标上的值和 word 的第 u 个字母不匹配则返回 false，如果当前匹配完了 word 的最后一个字母，则返回 true。
  3. 单层递归的逻辑：如果当前字母匹配成功，则标记已访问，并开始匹配下一个字母，依次枚举剩下的三个方向，继续递归匹配，如果匹配成功，则返回 true，否则三个方向都匹配失败返回 false。

时间复杂度

O(nm*3^k)，DFS 搜索的时间为 3^k，k 表示字符串的长度，最坏情况下每个点都要作为起点搜一遍，所以时间复杂度为 O(nm*3^k)。

空间复杂度

O(nm)

C++ 代码

class Solution {
public:
    vector<vector<char>> g;
    vector<vector<bool>> st;
    int n, m;
    int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};

    bool dfs(int x, int y, int u, string word) {
        if (g[x][y] != word[u]) return false;
        if (u == word.size() - 1) return true;

        st[x][y] = true;
        for (int i = 0; i < 4; i ++ ) {
            int a = x + dx[i], b = y + dy[i];
            if (a < 0 || a >= n || b < 0 || b >= m || st[a][b]) continue;
            if (dfs(a, b, u + 1, word)) return true;
        }
        st[x][y] = false;

        return false;
    }

    bool exist(vector<vector<char>>& board, string word) {
        g = board;
        n = g.size(), m = g[0].size();
        st = vector<vector<bool>>(n, vector<bool>(m, false));
        for (int i = 0; i < n; i ++ )
            for (int j = 0; j < m; j ++ )
                if (dfs(i, j, 0, word)) return true;
        return false;
    }
};

Java 代码

class Solution {
    private char[][] g;
    private boolean[][] st;
    private int n, m;
    private int[] dx = {-1, 0, 1, 0};
    private int[] dy = {0, 1, 0, -1};

    private boolean dfs(int x, int y, int u, String word) {
        if (g[x][y] != word.charAt(u)) {
            return false;
        }
        if (u == word.length() - 1) {
            return true;
        }

        st[x][y] = true;
        for (int i = 0; i < 4; i ++ ) {
            int a = x + dx[i], b = y + dy[i];
            if (a < 0 || a >= n || b < 0 || b >= m || st[a][b]) {
                continue;
            }
            if (dfs(a, b, u + 1, word)) {
                return true;
            }
        }
        st[x][y] = false;

        return false;
    }

    public boolean exist(char[][] board, String word) {
        g = board;
        n = g.length;
        m = g[0].length;
        st = new boolean[n][m];
        for (int i = 0; i < n; i ++ ) {
            for (int j = 0; j < m; j ++ ) {
                if (dfs(i, j, 0, word)) {
                    return true;
                }
            }
        }
        return false;
    }
}

Python 代码

class Solution:
    def exist(self, board: List[List[str]], word: str) -> bool:
        g = board
        n, m = len(g), len(g[0])
        st = [[False] * m for _ in range(n)]
        dx = [-1, 0, 1, 0]
        dy = [0, 1, 0, -1]

        def dfs(x, y, u):
            if g[x][y] != word[u]:
                return False
            if u == len(word) - 1:
                return True

            st[x][y] = True
            for i in range(4):
                a, b = x + dx[i], y + dy[i]
                if 0 <= a < n and 0 <= b < m and not st[a][b]:
                    if dfs(a, b, u + 1):
                        return True
            st[x][y] = False

            return False

        for i in range(n):
            for j in range(m):
                if dfs(i, j, 0):
                    return True
        return False

本文由读者提供，Github地址：https://github.com/tonngw

点击面试手册，获取本站面试手册PDF完整版

剑指offer