微信公众号：路人zhang
扫码关注微信公众号

回复“面试手册”，获取本站PDF版

回复“简历”，获取高质量简历模板

回复“加群”，加入程序员交流群

回复“电子书”，获取程序员类电子书

当前位置： 算法 > 剑指offer > 剑指offer 68-1. 二叉搜索树的最近公共祖先

剑指offer 68-1. 二叉搜索树的最近公共祖先

题目描述

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（ 一个节点也可以是它自己的祖先 ）。”

例如，给定如下二叉搜索树:  root = [6,2,8,0,4,7,9,null,null,3,5]

二叉搜索树

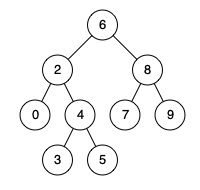
示例 1:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6 
解释: 节点 2 和节点 8 的最近公共祖先是 6。

示例 2:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

说明:

  • 所有节点的值都是唯一的。
  • p、q 为不同节点且均存在于给定的二叉搜索树中。

题解 1

(递归) O(h)

这道题目完全可以使用查找二叉树的最近公共祖先的方法去做，但是这种做法的时间复杂度是 O(n) 的，需要遍历整棵二叉树。对于二叉搜索树要充分利用它的有序特性，可以将时间复杂度优化为 O(h)。

由于二叉搜索树的有序性，从上往下遍历会比较方便，左边的都比根节点小，右边的都比根节点大。

递归三部曲：

  1. 递归函数的含义：返回以 root 为根节点的包含 p 和 q 的最近公共祖先，如果只包含一个就返回一个。
  2. 递归出口条件：如果当前节点为空，返回 NULL，但题目已知肯定存在答案，从上往下遍历的过程中不可能走到空节点，所以可以没有递归出口条件。
  3. 单层递归逻辑：
    • 如果 p 的值比 q 大，为了方便操作，首先交换一下两个节点的值，保证 p 的值小于 q 的值。
    • 如果当前节点的值大于等于 p 的值且小于等于 q 的值，那么当前节点就是 p 和 q 的最近公共祖先。
    • 如果当前节点的值大于等于 p 的值和 q 的值，说明答案一定在左子树中，所以递归搜索左子树。否则如果当前节点的值小于等于 p 的值和 q 的值，说明答案一定在右子树中，所以递归搜索右子树。

时间复杂度

由于二叉搜索树的有序性，答案要么在左边要么在右边，最坏情况下只需遍历从头节点到叶子节点的一条链，所以时间复杂度为 O(h)，h 为二叉搜索树的高度。

空间复杂度

O(n)

C++ 代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (p->val > q->val) swap(p, q);
        // 这里要加等于，因为当前节点可能是 p 或者 q，即 p 可能是 q 的祖先或者 q 是 p 的祖先
        if (p->val <= root->val && root->val <= q->val) return root;
        if (p->val < root->val && q->val < root->val) return lowestCommonAncestor(root->left, p, q);
        return lowestCommonAncestor(root->right, p, q);
    }
};

Java 代码

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if (p.val > q.val) {
            TreeNode temp = p;
            p = q;
            q = temp;
        }
        // 这里要加等于，因为当前节点可能是 p 或者 q，即 p 可能是 q 的祖先或者 q 是 p 的祖先
        if (p.val <= root.val && root.val <= q.val) {
            return root;
        }
        if (p.val < root.val && q.val < root.val) {
            return lowestCommonAncestor(root.left, p, q);
        }
        return lowestCommonAncestor(root.right, p, q);
    }
}

Python 代码

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def lowestCommonAncestor(self, root: TreeNode, p: TreeNode, q: TreeNode) -> TreeNode:
        if p.val > q.val:
            p, q = q, p
        # 这里要加等于，因为当前节点可能是 p 或者 q，即 p 可能是 q 的祖先或者 q 是 p 的祖先
        if p.val <= root.val <= q.val:
            return root
        if p.val < root.val and q.val < root.val:
            return self.lowestCommonAncestor(root.left, p, q)
        return self.lowestCommonAncestor(root.right, p, q)

本文由读者提供，Github地址：https://github.com/tonngw

点击面试手册，获取本站面试手册PDF完整版

剑指offer